New posts
They might've frozen my lower half, but my battle gear mounts on top
Loading...
Loading...
Written by DeepFriedUnicorn, 26.05.2025 at 10:56
Written by bilawi, 25.05.2025 at 09:45
Written by DeepFriedUnicorn, 21.05.2025 at 15:19
Another European Spring will happen. I might be there...
deppfried?
What is this font? Comic sands? My eyes hurt
its AI
Loading...
Loading...
Today in
New AtWar Calculator
A bit of explanation on how this works:
The CascadingRandom function (see https://atwar-game.com/forum/topic.php?topic_id=26143) has a nice probability distribution, here's the document I found which I wrote in like 2019 (although with a sign error in Eq. (5))

Since we have the probabilities of each roll, we approach this using a recursion/dynamic programming approach
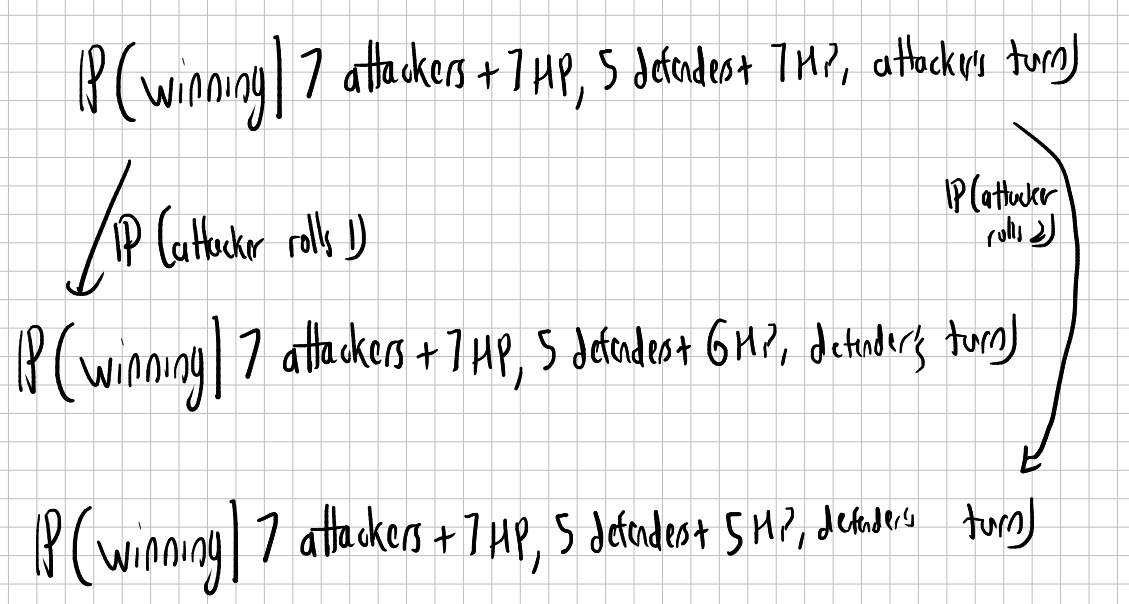
With boundary conditions being that when one unit count goes to 0, the probability of winning/losing is 1
(In case there's another physicist who is reading this but hasn't learnt about dynamic programming: Think path integral. This is basically a discrete time path integral. The path integral is the continuous time case of dynamic programming as related by the feynman-kac formula. I am computing the transition amplitude into a state where the battle is won.)
The TODOS are
1. GUI
2. Figure out why the results don't match with the online calculator
3. Parallelisation to make it faster https://www.sciencedirect.com/science/article/abs/pii/S0743731510000110?via%3Dihub
The CascadingRandom function (see https://atwar-game.com/forum/topic.php?topic_id=26143) has a nice probability distribution, here's the document I found which I wrote in like 2019 (although with a sign error in Eq. (5))

Since we have the probabilities of each roll, we approach this using a recursion/dynamic programming approach
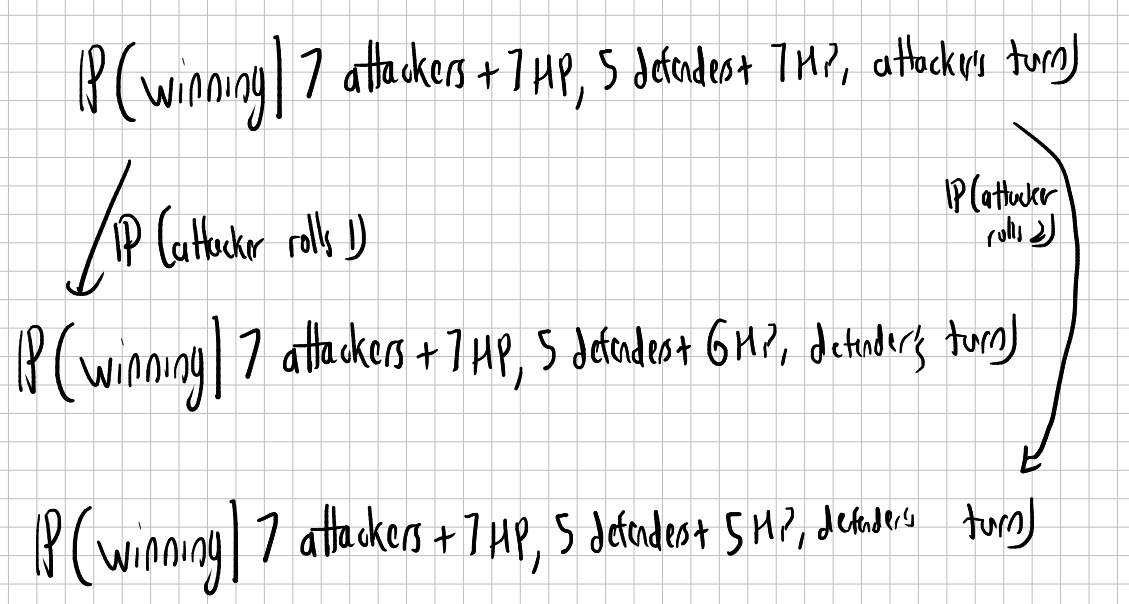
With boundary conditions being that when one unit count goes to 0, the probability of winning/losing is 1
(In case there's another physicist who is reading this but hasn't learnt about dynamic programming: Think path integral. This is basically a discrete time path integral. The path integral is the continuous time case of dynamic programming as related by the feynman-kac formula. I am computing the transition amplitude into a state where the battle is won.)
The TODOS are
1. GUI
2. Figure out why the results don't match with the online calculator
3. Parallelisation to make it faster https://www.sciencedirect.com/science/article/abs/pii/S0743731510000110?via%3Dihub
Loading...
Loading...
Today in
New AtWar Calculator
Written by LukeTan, Today at 07:41
yap yap yap
thanks for this luke, i dont understand it yet but i will soon
Loading...
Loading...
Today in
New AtWar Calculator
I recently found a document I wrote dating back to 2019 about making an atwar calculator; I decided not to let my past efforts go to waste.
Pros and Cons
Pros:
Calculator is exact (no simulations!)
This means that it can reach results a lot more exact than the other calculators, especially when probabilities are in the high 90%s and high precision is demanded.
There is absolutely no scaling with the precision, no need to run more simulations
Support for arbitrary unit types
Cons:
No GUI and not even a CLI, only code (attached below, written in C++)
I don't code so I don't know how to make a GUI.
Relatively high memory usage (N1 * N2 * MAX_HP^2) space, this means it should take up to 100 units on each side to reach 1MB, but the simulation based calculators basically store only 1 int so...
Only battles with 2 stacks because I don't know how 3+ stack battles work
I don't know if it works (see below)
Honestly this was as much an academic curiosity as it was an actual thing, I'll probably use it but there isn't any significant benefit over the old ones.
Results
I compare my calculator, the online calculator https://atwar-game.com/sim/ and clovis's old calculator https://atwar-game.com/forum/topic.php?topic_id=27835, 100000 simulations online calculator, 1000000 on clovis's desktop calculator
1 tank vs 1 inf, no upgrades
Mine: 0.539516086002
Online: 0.5380
Desktop: 0.475936
2 tanks vs 2 infs, no upgrades
Mine: 0.641423918197
Online: 0.6709
Desktop: 0.57925
3 tanks vs 3 infs, no upgrades
Mine: 0.718264486868
Online: 0.7494
Desktop: 0.652268
4 tanks vs 4 infs, no upgrades
Mine: 0.776176525286
Online: 0.8005
Desktop: 0.704646
5 tanks vs 5 infs, no upgrades
Mine: 0.819253328953
Online: 0.8398
Desktop: 0.744511
6 tanks vs 6 infs, no upgrades
Mine: 0.851735764890
Online: 0.8707
Desktop: 0.777521
7 tanks vs 7 infs, no upgrades
Mine: 0.877327988814
Online: 0.8920
Desktop: 0.804569
8 tanks vs 8 infs, no upgrades
Mine: 0.897951262811
Online: 0.9088
Desktop: 0.827188
If you plot the above results, you get something like this
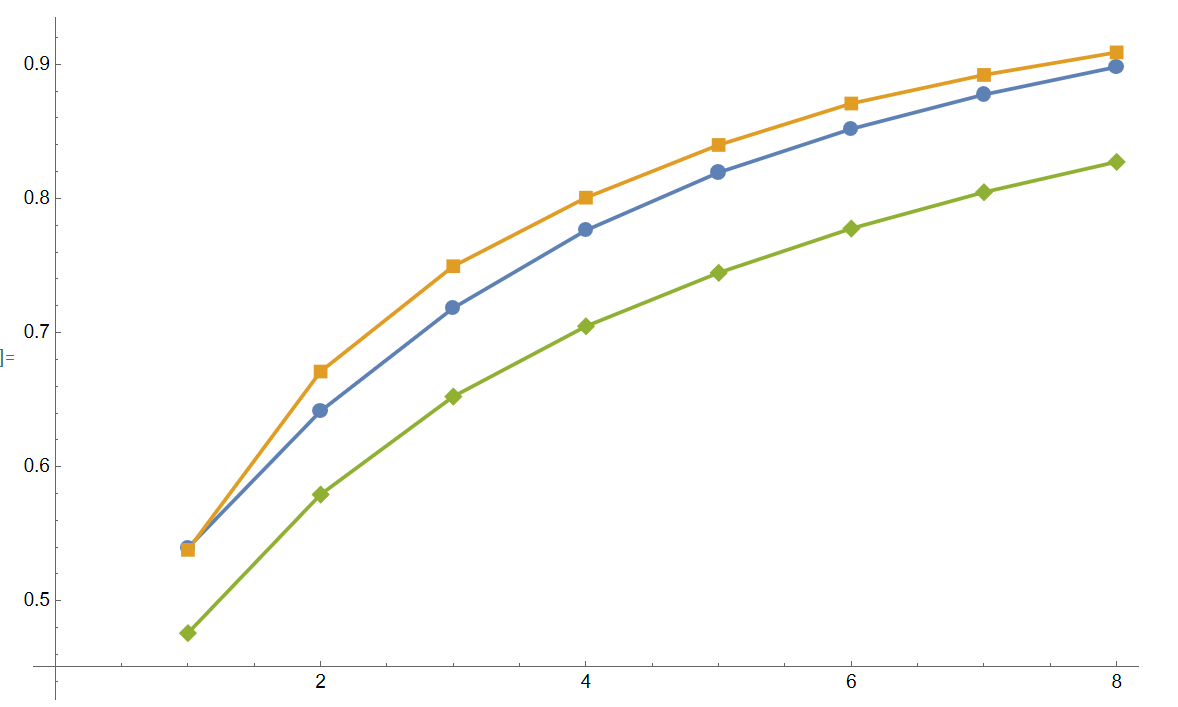
Note that the statistical error is smaller than the point (being <= 0.002 for the online calculator), so they aren't actually giving the same result.
What might be interesting to some is
6 infs vs 4 mils, no upgrades
Mine: 0.992415070266
Online: 0.9972
8 infs vs 6 mils, no upgrades
Mine: 0.984068658257
Online: 0.9936
Also
SM 7 bombs 3 infs vs 8 infs, no upgrades
Mine: 0.946704205647
Online: 0.9637
So that is clearly not good enough, not that anyone plays SM anymore, but if you do stop sending 7 bombers to moscow
To compare time:
50 infs 50 tanks vs 100 infs, no upgrades
Online with 10000 simulations: 0.5058, took approximately 13 seconds, the statistical error is 0.005
Mine: 0.472166945505, took 2.978 seconds with -O3 optimisation
Epilogue
I know this is coming so I'll post it in advance

Code!
#include <cstdio>
#include <vector>
#include <map>
#include <string>
#include <algorithm>
#include <iostream>
#include <math.h>
using namespace std;
class unitType{
public:
unitType(string x, int y, int z, int w, int r, map<string, int> defBonus2){
name = x;
atk = y;
def = z;
hp = w;
crit = r;
defBonus = defBonus2;
}
string name;
int atk;
int def;
int hp;
int crit;
map<string, int> defBonus;
};
// Comparison functor for sorting by atk
struct CompareByAtk {
bool operator()(const unitType& lhs, const unitType& rhs) const {
return lhs.atk < rhs.atk;
}
};
// Comparison functor for sorting by def
struct CompareByDef {
bool operator()(const unitType& lhs, const unitType& rhs) const {
return lhs.def < rhs.def;
}
};
inline double stackingBonus(int totAtk, int atkUnit, int totDef, int defUnit, int defBonus){
return (double) (totAtk + atkUnit)/(totDef + defUnit + defBonus);
}
class Calculator{
public:
Calculator(map<unitType, int, CompareByAtk> atk, map<unitType, int, CompareByDef> def){
atkStack = atk;
defStack = def;
N1 = 0;
N2 = 0;
for (auto it = atkStack.begin(); it != atkStack.end(); ++it){
N1 += (*it).second;
HP_MAX = max((*it).first.hp, HP_MAX);
}
for (auto it = defStack.begin(); it != defStack.end(); ++it){
N2 += (*it).second;
HP_MAX = max((*it).first.hp, HP_MAX);
}
dp = vector<vector<vector<vector<vector<double>>>>>(N1+1, vector<vector<vector<vector<double>>>>(HP_MAX+1, vector<vector<vector<double>>>(N2+1, vector<vector<double>>(HP_MAX+1, vector<double>(2, -1)))));
runSumAtk = vector<int>(1,0);
for (auto it = atkStack.begin(); it != atkStack.end(); ++it) runSumAtk.push_back(runSumAtk.back() + (*it).second);
runSumDef = vector<int>(1,0);
for (auto it = defStack.begin(); it != defStack.end(); ++it) runSumDef.push_back(runSumDef.back() + (*it).second);
//for (int i = 0; i < (int)runSumAtk.size(); ++i) printf("%d ", runSumAtk[i]); printf("n");
}
private:
map<unitType, int, CompareByAtk> atkStack;
map<unitType, int, CompareByDef> defStack;
int N1;
int N2;
int HP_MAX;
//dynamic programming array, n1, hp1, n2, hp2
vector<vector<vector<vector<vector<double>>>>> dp;
//given n, i want to know what unit is up front
vector<int> runSumAtk;
vector<int> runSumDef;
unitType frontAttackUnit(int n){
auto it = lower_bound(runSumAtk.begin(), runSumAtk.end(), n);
// The index is the position before upper_bound
int ind = std::distance(runSumAtk.begin(), it) - 1;
auto it2 = atkStack.begin();
advance(it2, ind);
return (*it2).first;
}
unitType frontDefenceUnit(int n){
auto it = lower_bound(runSumDef.begin(), runSumDef.end(), n);
// The index is the position before upper_bound
int ind = std::distance(runSumDef.begin(), it) - 1;
auto it2 = defStack.begin();
advance(it2, ind);
return (*it2).first;
}
int totAtk(int n){
auto it = lower_bound(runSumAtk.begin(), runSumAtk.end(), n);
int ind = std::distance(runSumAtk.begin(), it) - 1;
int ans = 0;
auto it2 = atkStack.begin();
int currAtk = 0;
for (int i = 0; i <= ind - 1; ++i){
currAtk = (*it2).first.atk;
ans += currAtk * (*it2).second;
advance(it2, 1);
}
currAtk = (*it2).first.atk;
ans += currAtk * (n - runSumAtk[ind]);
return ans;
}
int totDef(int n){
auto it = lower_bound(runSumDef.begin(), runSumDef.end(), n);
int ind = std::distance(runSumDef.begin(), it) - 1;
int ans = 0;
auto it2 = defStack.begin();
int currDef = 0;
for (int i = 0; i <= ind - 1; ++i){
currDef = (*it2).first.def;
ans += currDef * (*it2).second;
advance(it2, 1);
}
currDef = (*it2).first.def;
ans += currDef * (n - runSumDef[ind]);
return ans;
}
public:
//this is prob of attacker winning
//1 if it's the attacker's turn, 0 otherwise
double probability(int n1, int hp1, int n2, int hp2, int attackTurn){
if (n1 == 0) return 0;
else if (n2 == 0) return 1;
else if (dp[n1][hp1][n2][hp2][attackTurn] != -1) return dp[n1][hp1][n2][hp2][attackTurn];
else {
//compute defence bonus
unitType frontAtkUnit = frontAttackUnit(n1);
unitType frontDefUnit = frontDefenceUnit(n2);
int defBonus = 0;
if (frontDefUnit.defBonus.count(frontAtkUnit.name)) defBonus = frontDefUnit.defBonus[frontAtkUnit.name];
//compute total attack and defence
int totalAttack = totAtk(n1);
int totalDefence = totDef(n2);
//multiplier
double difference = stackingBonus(totalAttack, n1, totalDefence, n2, defBonus);
double prob = 0;
double reducer = 0;
double rollProb = 0;
if (attackTurn){
if (difference < 1) reducer = (difference+1.0)/(2.0);
else {rollProb = (double)1/frontAtkUnit.atk; reducer = -1;} //i use -1 instead of 1 so that there is less chance of numerical error
for (int roll = 1; roll <= frontAtkUnit.atk; ++roll){
if (reducer != -1) rollProb = pow(reducer, roll) * (1.0 - reducer)/(reducer*(1 - pow(reducer, frontAtkUnit.atk)));
for (int crit = 0; crit <= 1; ++crit){
int roll2 = roll + crit*frontAtkUnit.atk;
int hpAfter = hp2 - roll2;
if (hpAfter <= 0){
int unitsKilled = 0;
while (hpAfter <= 0)
{
unitsKilled++;
if (n2 - unitsKilled <= 0) break;
unitType nextUnit = frontDefenceUnit(n2-unitsKilled);
hpAfter += nextUnit.hp;
}
double result = rollProb*probability(n1, hp1, n2-unitsKilled, hpAfter, 1-attackTurn);
double critProb = (double) frontAtkUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
} else {
double result = rollProb*probability(n1, hp1, n2, hpAfter, 1-attackTurn);
double critProb = (double) frontAtkUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
}
}
}
} else {
//printf("difference = %.5fn",difference);
if (difference > 1) reducer = (difference+1.0)/(2.0*difference);
else {rollProb = (double)1/frontDefUnit.def; reducer = -1;} //i use -1 instead of 1 so that there is less chance of numerical error
//printf("reducer = %.5fn",reducer);
for (int roll = 1; roll <= frontDefUnit.def; ++roll){
if (reducer != -1) rollProb = pow(reducer, roll) * (1.0 - reducer)/(reducer*(1 - pow(reducer, frontDefUnit.def)));
for (int crit = 0; crit <= 1; ++crit){
int roll2 = roll + crit*frontDefUnit.def;
int hpAfter = hp1 - roll2;
if (hpAfter <= 0){
int unitsKilled = 0;
while (hpAfter <= 0)
{
unitsKilled++;
if (n1 - unitsKilled <= 0) break;
unitType nextUnit = frontAttackUnit(n1-unitsKilled);
hpAfter += nextUnit.hp;
}
double result = rollProb*probability(n1-unitsKilled, hpAfter, n2, hp2, 1-attackTurn);
double critProb = (double) frontDefUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
} else {
double result = rollProb*probability(n1, hpAfter, n2, hp2, 1-attackTurn);
double critProb = (double) frontDefUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
}
}
}
};
return dp[n1][hp1][n2][hp2][attackTurn] = prob;
}
}
double calculate(){
unitType frontAtkUnit2 = this->frontAttackUnit(this->N1);
unitType frontDefUnit2 = this->frontDefenceUnit(this->N2);
return probability(this->N1, frontAtkUnit2.hp, this->N2, frontDefUnit2.hp, 0);
}
void print(){
printf("Attacker's stack:n");
for (auto it = atkStack.begin(); it != atkStack.end(); ++it) cout << (*it).first.name << ": " << (*it).second << endl;
printf("Total number of units: %dn", this -> N1);
printf("Defender's stack:n");
for (auto it = defStack.begin(); it != defStack.end(); ++it) cout << (*it).first.name << ": " << (*it).second << endl;
printf("Total number of units: %dn", this -> N2);
printf("Max HP: %dn", this->HP_MAX);
}
};
//we just define the unit types here as globals cos why the hell not
unitType inf("inf", 4, 6, 7, 5, map<string, int>{{"heli", -2}});
unitType tank("tank", 8, 4, 7, 5, map<string, int>{});
unitType DSheli("heli", 8, 3, 7, 5, map<string, int>{});
unitType gen("gen", 2, 2, 2, 0, map<string, int>{});
unitType mil("mil", 3, 4, 7, 2, map<string, int>{{"heli", -1}});
unitType SMbomb("bomb", 8, 5, 7, 7, map<string, int>{});
unitType SMinf("inf", 3, 6, 7, 3, map<string, int>{{"heli", -2}});
int main(){
Calculator calculator(map<unitType, int, CompareByAtk>{{SMinf, 3}, {SMbomb, 7}}, map<unitType, int, CompareByDef>{{inf, 8}});
calculator.print();
printf("Result: %.12f", calculator.calculate());
return 0;
}
Pros and Cons
Pros:
Calculator is exact (no simulations!)
This means that it can reach results a lot more exact than the other calculators, especially when probabilities are in the high 90%s and high precision is demanded.
There is absolutely no scaling with the precision, no need to run more simulations
Support for arbitrary unit types
Cons:
No GUI and not even a CLI, only code (attached below, written in C++)
I don't code so I don't know how to make a GUI.
Relatively high memory usage (N1 * N2 * MAX_HP^2) space, this means it should take up to 100 units on each side to reach 1MB, but the simulation based calculators basically store only 1 int so...
Only battles with 2 stacks because I don't know how 3+ stack battles work
I don't know if it works (see below)
Honestly this was as much an academic curiosity as it was an actual thing, I'll probably use it but there isn't any significant benefit over the old ones.
Results
I compare my calculator, the online calculator https://atwar-game.com/sim/ and clovis's old calculator https://atwar-game.com/forum/topic.php?topic_id=27835, 100000 simulations online calculator, 1000000 on clovis's desktop calculator
1 tank vs 1 inf, no upgrades
Mine: 0.539516086002
Online: 0.5380
Desktop: 0.475936
2 tanks vs 2 infs, no upgrades
Mine: 0.641423918197
Online: 0.6709
Desktop: 0.57925
3 tanks vs 3 infs, no upgrades
Mine: 0.718264486868
Online: 0.7494
Desktop: 0.652268
4 tanks vs 4 infs, no upgrades
Mine: 0.776176525286
Online: 0.8005
Desktop: 0.704646
5 tanks vs 5 infs, no upgrades
Mine: 0.819253328953
Online: 0.8398
Desktop: 0.744511
6 tanks vs 6 infs, no upgrades
Mine: 0.851735764890
Online: 0.8707
Desktop: 0.777521
7 tanks vs 7 infs, no upgrades
Mine: 0.877327988814
Online: 0.8920
Desktop: 0.804569
8 tanks vs 8 infs, no upgrades
Mine: 0.897951262811
Online: 0.9088
Desktop: 0.827188
If you plot the above results, you get something like this

Note that the statistical error is smaller than the point (being <= 0.002 for the online calculator), so they aren't actually giving the same result.
What might be interesting to some is
6 infs vs 4 mils, no upgrades
Mine: 0.992415070266
Online: 0.9972
8 infs vs 6 mils, no upgrades
Mine: 0.984068658257
Online: 0.9936
Also
SM 7 bombs 3 infs vs 8 infs, no upgrades
Mine: 0.946704205647
Online: 0.9637
So that is clearly not good enough, not that anyone plays SM anymore, but if you do stop sending 7 bombers to moscow
To compare time:
50 infs 50 tanks vs 100 infs, no upgrades
Online with 10000 simulations: 0.5058, took approximately 13 seconds, the statistical error is 0.005
Mine: 0.472166945505, took 2.978 seconds with -O3 optimisation
Epilogue
I know this is coming so I'll post it in advance

Code!
#include <cstdio>
#include <vector>
#include <map>
#include <string>
#include <algorithm>
#include <iostream>
#include <math.h>
using namespace std;
class unitType{
public:
unitType(string x, int y, int z, int w, int r, map<string, int> defBonus2){
name = x;
atk = y;
def = z;
hp = w;
crit = r;
defBonus = defBonus2;
}
string name;
int atk;
int def;
int hp;
int crit;
map<string, int> defBonus;
};
// Comparison functor for sorting by atk
struct CompareByAtk {
bool operator()(const unitType& lhs, const unitType& rhs) const {
return lhs.atk < rhs.atk;
}
};
// Comparison functor for sorting by def
struct CompareByDef {
bool operator()(const unitType& lhs, const unitType& rhs) const {
return lhs.def < rhs.def;
}
};
inline double stackingBonus(int totAtk, int atkUnit, int totDef, int defUnit, int defBonus){
return (double) (totAtk + atkUnit)/(totDef + defUnit + defBonus);
}
class Calculator{
public:
Calculator(map<unitType, int, CompareByAtk> atk, map<unitType, int, CompareByDef> def){
atkStack = atk;
defStack = def;
N1 = 0;
N2 = 0;
for (auto it = atkStack.begin(); it != atkStack.end(); ++it){
N1 += (*it).second;
HP_MAX = max((*it).first.hp, HP_MAX);
}
for (auto it = defStack.begin(); it != defStack.end(); ++it){
N2 += (*it).second;
HP_MAX = max((*it).first.hp, HP_MAX);
}
dp = vector<vector<vector<vector<vector<double>>>>>(N1+1, vector<vector<vector<vector<double>>>>(HP_MAX+1, vector<vector<vector<double>>>(N2+1, vector<vector<double>>(HP_MAX+1, vector<double>(2, -1)))));
runSumAtk = vector<int>(1,0);
for (auto it = atkStack.begin(); it != atkStack.end(); ++it) runSumAtk.push_back(runSumAtk.back() + (*it).second);
runSumDef = vector<int>(1,0);
for (auto it = defStack.begin(); it != defStack.end(); ++it) runSumDef.push_back(runSumDef.back() + (*it).second);
//for (int i = 0; i < (int)runSumAtk.size(); ++i) printf("%d ", runSumAtk[i]); printf("n");
}
private:
map<unitType, int, CompareByAtk> atkStack;
map<unitType, int, CompareByDef> defStack;
int N1;
int N2;
int HP_MAX;
//dynamic programming array, n1, hp1, n2, hp2
vector<vector<vector<vector<vector<double>>>>> dp;
//given n, i want to know what unit is up front
vector<int> runSumAtk;
vector<int> runSumDef;
unitType frontAttackUnit(int n){
auto it = lower_bound(runSumAtk.begin(), runSumAtk.end(), n);
// The index is the position before upper_bound
int ind = std::distance(runSumAtk.begin(), it) - 1;
auto it2 = atkStack.begin();
advance(it2, ind);
return (*it2).first;
}
unitType frontDefenceUnit(int n){
auto it = lower_bound(runSumDef.begin(), runSumDef.end(), n);
// The index is the position before upper_bound
int ind = std::distance(runSumDef.begin(), it) - 1;
auto it2 = defStack.begin();
advance(it2, ind);
return (*it2).first;
}
int totAtk(int n){
auto it = lower_bound(runSumAtk.begin(), runSumAtk.end(), n);
int ind = std::distance(runSumAtk.begin(), it) - 1;
int ans = 0;
auto it2 = atkStack.begin();
int currAtk = 0;
for (int i = 0; i <= ind - 1; ++i){
currAtk = (*it2).first.atk;
ans += currAtk * (*it2).second;
advance(it2, 1);
}
currAtk = (*it2).first.atk;
ans += currAtk * (n - runSumAtk[ind]);
return ans;
}
int totDef(int n){
auto it = lower_bound(runSumDef.begin(), runSumDef.end(), n);
int ind = std::distance(runSumDef.begin(), it) - 1;
int ans = 0;
auto it2 = defStack.begin();
int currDef = 0;
for (int i = 0; i <= ind - 1; ++i){
currDef = (*it2).first.def;
ans += currDef * (*it2).second;
advance(it2, 1);
}
currDef = (*it2).first.def;
ans += currDef * (n - runSumDef[ind]);
return ans;
}
public:
//this is prob of attacker winning
//1 if it's the attacker's turn, 0 otherwise
double probability(int n1, int hp1, int n2, int hp2, int attackTurn){
if (n1 == 0) return 0;
else if (n2 == 0) return 1;
else if (dp[n1][hp1][n2][hp2][attackTurn] != -1) return dp[n1][hp1][n2][hp2][attackTurn];
else {
//compute defence bonus
unitType frontAtkUnit = frontAttackUnit(n1);
unitType frontDefUnit = frontDefenceUnit(n2);
int defBonus = 0;
if (frontDefUnit.defBonus.count(frontAtkUnit.name)) defBonus = frontDefUnit.defBonus[frontAtkUnit.name];
//compute total attack and defence
int totalAttack = totAtk(n1);
int totalDefence = totDef(n2);
//multiplier
double difference = stackingBonus(totalAttack, n1, totalDefence, n2, defBonus);
double prob = 0;
double reducer = 0;
double rollProb = 0;
if (attackTurn){
if (difference < 1) reducer = (difference+1.0)/(2.0);
else {rollProb = (double)1/frontAtkUnit.atk; reducer = -1;} //i use -1 instead of 1 so that there is less chance of numerical error
for (int roll = 1; roll <= frontAtkUnit.atk; ++roll){
if (reducer != -1) rollProb = pow(reducer, roll) * (1.0 - reducer)/(reducer*(1 - pow(reducer, frontAtkUnit.atk)));
for (int crit = 0; crit <= 1; ++crit){
int roll2 = roll + crit*frontAtkUnit.atk;
int hpAfter = hp2 - roll2;
if (hpAfter <= 0){
int unitsKilled = 0;
while (hpAfter <= 0)
{
unitsKilled++;
if (n2 - unitsKilled <= 0) break;
unitType nextUnit = frontDefenceUnit(n2-unitsKilled);
hpAfter += nextUnit.hp;
}
double result = rollProb*probability(n1, hp1, n2-unitsKilled, hpAfter, 1-attackTurn);
double critProb = (double) frontAtkUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
} else {
double result = rollProb*probability(n1, hp1, n2, hpAfter, 1-attackTurn);
double critProb = (double) frontAtkUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
}
}
}
} else {
//printf("difference = %.5fn",difference);
if (difference > 1) reducer = (difference+1.0)/(2.0*difference);
else {rollProb = (double)1/frontDefUnit.def; reducer = -1;} //i use -1 instead of 1 so that there is less chance of numerical error
//printf("reducer = %.5fn",reducer);
for (int roll = 1; roll <= frontDefUnit.def; ++roll){
if (reducer != -1) rollProb = pow(reducer, roll) * (1.0 - reducer)/(reducer*(1 - pow(reducer, frontDefUnit.def)));
for (int crit = 0; crit <= 1; ++crit){
int roll2 = roll + crit*frontDefUnit.def;
int hpAfter = hp1 - roll2;
if (hpAfter <= 0){
int unitsKilled = 0;
while (hpAfter <= 0)
{
unitsKilled++;
if (n1 - unitsKilled <= 0) break;
unitType nextUnit = frontAttackUnit(n1-unitsKilled);
hpAfter += nextUnit.hp;
}
double result = rollProb*probability(n1-unitsKilled, hpAfter, n2, hp2, 1-attackTurn);
double critProb = (double) frontDefUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
} else {
double result = rollProb*probability(n1, hpAfter, n2, hp2, 1-attackTurn);
double critProb = (double) frontDefUnit.crit/100.0;
prob += crit ? critProb*result : (1-critProb)*result;
}
}
}
};
return dp[n1][hp1][n2][hp2][attackTurn] = prob;
}
}
double calculate(){
unitType frontAtkUnit2 = this->frontAttackUnit(this->N1);
unitType frontDefUnit2 = this->frontDefenceUnit(this->N2);
return probability(this->N1, frontAtkUnit2.hp, this->N2, frontDefUnit2.hp, 0);
}
void print(){
printf("Attacker's stack:n");
for (auto it = atkStack.begin(); it != atkStack.end(); ++it) cout << (*it).first.name << ": " << (*it).second << endl;
printf("Total number of units: %dn", this -> N1);
printf("Defender's stack:n");
for (auto it = defStack.begin(); it != defStack.end(); ++it) cout << (*it).first.name << ": " << (*it).second << endl;
printf("Total number of units: %dn", this -> N2);
printf("Max HP: %dn", this->HP_MAX);
}
};
//we just define the unit types here as globals cos why the hell not
unitType inf("inf", 4, 6, 7, 5, map<string, int>{{"heli", -2}});
unitType tank("tank", 8, 4, 7, 5, map<string, int>{});
unitType DSheli("heli", 8, 3, 7, 5, map<string, int>{});
unitType gen("gen", 2, 2, 2, 0, map<string, int>{});
unitType mil("mil", 3, 4, 7, 2, map<string, int>{{"heli", -1}});
unitType SMbomb("bomb", 8, 5, 7, 7, map<string, int>{});
unitType SMinf("inf", 3, 6, 7, 3, map<string, int>{{"heli", -2}});
int main(){
Calculator calculator(map<unitType, int, CompareByAtk>{{SMinf, 3}, {SMbomb, 7}}, map<unitType, int, CompareByDef>{{inf, 8}});
calculator.print();
printf("Result: %.12f", calculator.calculate());
return 0;
}
Loading...
Loading...
07.06.2025 in
Casual Saturdays
Casual Saturday #43 - Colonial Supremacy
Standard settings
https://atwar-game.com/games/?link=0168488379
Standard settings
https://atwar-game.com/games/?link=0168488379
Loading...
Loading...
05.06.2025 in
Hack in Atwar
Ofc is needed, battle screen for kislev would show everything , its kinda sus that is not included, not gonna lie
Loading...
Loading...
04.06.2025 in
Hack in Atwar
Written by DON RUTTER, 04.06.2025 at 19:46
I would say even with all the proof being provided, it is not enough. There is still a possibility that it was a glitch, and he is trolling (Puchao is a known troll). Hence, if that possibility and doubt still exists, we cannot condemn him (at least the public).
I think developers and mods who know more about the game and these type of stuff should be ones investigating for more precision. They could say or explain if the game was hacked in this situation. But so far, no response from them.
Silence noob u doomed me on the game u was Poland....why the heck did you leave???
Loading...
Loading...
04.06.2025 in
Hack in Atwar
I would say even with all the proof being provided, it is not enough. There is still a possibility that it was a glitch, and he is trolling (Puchao is a known troll). Hence, if that possibility and doubt still exists, we cannot condemn him (at least the public).
I think developers and mods who know more about the game and these type of stuff should be ones investigating for more precision. They could say or explain if the game was hacked in this situation. But so far, no response from them.
I think developers and mods who know more about the game and these type of stuff should be ones investigating for more precision. They could say or explain if the game was hacked in this situation. But so far, no response from them.
Loading...
Loading...
04.06.2025 in
Hack in Atwar
Sometimes whole stack follows one unit if u put those units around kiev in the city and he attacked the unit it glitches but we dont have ss of the unit movements to see what happened , but i believe u abi
Loading...
Loading...
04.06.2025 in
For arabs and muslims only للعرب والمسلمين فقط
Inshallah my brother
Loading...
Loading...
Written by Metyu, 04.06.2025 at 06:52
Written by GREAT_ALGERIA123, 02.06.2025 at 02:58
"To all Arabs and Muslims, we cordially invite you to join our alliance, 'Arabs and Muslims'. Let us unite under one banner."
إلى جميع العرب والمسلمين، ندعوكم للانضمام إلى تحالفنا "العرب والمسلمين". فلنتحد تحت راية واحدة.
Algeria is not against Iraq
Loading...
Loading...
04.06.2025 in
For arabs and muslims only للعرب والمسلمين فقط
Written by GREAT_ALGERIA123, 02.06.2025 at 02:58
"To all Arabs and Muslims, we cordially invite you to join our alliance, 'Arabs and Muslims'. Let us unite under one banner."
إلى جميع العرب والمسلمين، ندعوكم للانضمام إلى تحالفنا "العرب والمسلمين". فلنتحد تحت راية واحدة.
Loading...
Loading...
04.06.2025 in
Hack in Atwar
Written by Grand Inquisitor, 04.06.2025 at 01:09
CW then , you even gonna be soo good and play us at scen ,just we soo shity?
CW with who? I'm in an inactive clan who played competitive only.. I literally started playing scenarios after years of absence solely because of how dead the game is and frankly I'm not impressed.
Loading...
Loading...
04.06.2025 in
Hack in Atwar
Written by Augustus Caesar, 03.06.2025 at 18:03
No wonder why the majority of scenario players are dogshit. Half the people in here commenting are just sword swallowing massaging each others tips going "ahh yes we is so gud at stacking trench mmmmm" You have a prominent player admitting to abusing an exploit because he got stomped with relative ease and all the collective hive mind can say is "hurrrr culd be glitch u mad hurrrr"
CW then , you even gonna be soo good and play us at scen ,just we soo shity?
Loading...
Loading...
03.06.2025 in
Hack in Atwar
Quote:Written by sirivann, 03.06.2025 at 21:12
stfu too u bitchas xD
Bro you're EZ
Loading...
Loading...
03.06.2025 in
Hack in Atwar
Written by Hi_I_am_Eren, 03.06.2025 at 11:41
Written by sirivann, 02.06.2025 at 21:11
Written by Hi_I_am_Eren, 02.06.2025 at 06:56
Written by sirivann, 01.06.2025 at 22:29
Written by Hi_I_am_Eren, 01.06.2025 at 16:47
Written by sirivann, 01.06.2025 at 14:43
Stop crying eren u nab
Did u read forum ? Did u looked ss ? Why this prejudice?
With all the games ive had, several times my army has glitched and ended up in a further battle so thats a option, theres also around 3 different range glitchs. Nothing new hence why i say that lol
Do u think it is glitches or samething ? If u realy think like that u didn't read my forum. Attaking Kiev from Minsk in one turn is not glitched. It is just range hack.
Ive read your post and ive seen that glitch in ww1 lots of times when armies teleport to big battles/viceversa or as i said it can be a mix of the 3 range bugs, stop being close minded and think its hax just cuz someone is baiting in chat lol we have all said that when glitchs happen too xD
Even Puchao accepts he hacked. I can't believe, u still say it is glitch
im not saying it was im saying theres multiple things that it could be, if ur so sure its hax tell admins/mod let them do there job lol
PS: Next time post a SS of the unit movement at the start of the turn its easier seeing how turn went that way for ppl who werent in the game.
Loading...
Loading...
03.06.2025 in
Hack in Atwar
Written by Augustus Caesar, 03.06.2025 at 18:03
No wonder why the majority of scenario players are dogshit. Half the people in here commenting are just sword swallowing massaging each others tips going "ahh yes we is so gud at stacking trench mmmmm" You have a prominent player admitting to abusing an exploit because he got stomped with relative ease and all the collective hive mind can say is "hurrrr culd be glitch u mad hurrrr"
stfu too u bitchas xD
Loading...
Loading...
03.06.2025 in
Hack in Atwar
No wonder why the majority of scenario players are dogshit. Half the people in here commenting are just sword swallowing massaging each others tips going "ahh yes we is so gud at stacking trench mmmmm" You have a prominent player admitting to abusing an exploit because he got stomped with relative ease and all the collective hive mind can say is "hurrrr culd be glitch u mad hurrrr"
Loading...
Loading...
Loading...
Loading...
03.06.2025 in
Hack in Atwar
Written by sirivann, 02.06.2025 at 21:11
Written by Hi_I_am_Eren, 02.06.2025 at 06:56
Written by sirivann, 01.06.2025 at 22:29
Written by Hi_I_am_Eren, 01.06.2025 at 16:47
Written by sirivann, 01.06.2025 at 14:43
Stop crying eren u nab
Did u read forum ? Did u looked ss ? Why this prejudice?
With all the games ive had, several times my army has glitched and ended up in a further battle so thats a option, theres also around 3 different range glitchs. Nothing new hence why i say that lol
Do u think it is glitches or samething ? If u realy think like that u didn't read my forum. Attaking Kiev from Minsk in one turn is not glitched. It is just range hack.
Ive read your post and ive seen that glitch in ww1 lots of times when armies teleport to big battles/viceversa or as i said it can be a mix of the 3 range bugs, stop being close minded and think its hax just cuz someone is baiting in chat lol we have all said that when glitchs happen too xD
Even Puchao accepts he hacked. I can't believe, u still say it is glitch


Loading...
Loading...
02.06.2025 in
Hack in Atwar
Written by Hi_I_am_Eren, 02.06.2025 at 06:56
Written by sirivann, 01.06.2025 at 22:29
Written by Hi_I_am_Eren, 01.06.2025 at 16:47
Written by sirivann, 01.06.2025 at 14:43
Stop crying eren u nab
Did u read forum ? Did u looked ss ? Why this prejudice?
With all the games ive had, several times my army has glitched and ended up in a further battle so thats a option, theres also around 3 different range glitchs. Nothing new hence why i say that lol
Do u think it is glitches or samething ? If u realy think like that u didn't read my forum. Attaking Kiev from Minsk in one turn is not glitched. It is just range hack.
Ive read your post and ive seen that glitch in ww1 lots of times when armies teleport to big battles/viceversa or as i said it can be a mix of the 3 range bugs, stop being close minded and think its hax just cuz someone is baiting in chat lol we have all said that when glitchs happen too xD
Loading...
Loading...
02.06.2025 in
For arabs and muslims only للعرب والمسلمين فقط
Never watch this video pal
Loading...
Loading...

 ?????????????
?????????????





